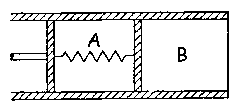
El volumen cilíndrico de la figura, de sección constante S=1 m2, consta de dos cámaras A y B separadas entre sí por un pistón que a su vez va unido mediante un resorte lineal de constante elástica k=3 N/m a otro pistón provisto de un vástago. El compartimento A contiene helio y el B nitrógeno molecular. La superficie lateral del cilindro es impermeable al calor, lo mismo que los pistones, pero en cambio la base del rectángulo que limita el compartimento B es perfectamente permeable al calor. Inicialmente los dos compartimentos tienen el mismo volumen Vo=2 m3 y la misma presión Po=105 N/m2, siendo su temperatura inicial también la misma e igual a la temperatura constante de la atmósfera exterior. Muy lentamente se va desplazando el vástago hacia la derecha hasta llegar a un estado final en el que la presión en el compartimento A duplica su valor inicial. Sabiendo que los dos pistones se pueden mover sin ningún rozamiento a lo largo del cilindro y que el resorte está inicialmente descargado, se desea calcular el trabajo mecánico que es preciso realizar para hacer esa transformación.