Problemas

Un sistema óptico centrado está formado por dos lentes delgadas L1 y L2 y un espejo esférico E, situados en ese orden. La distancia entre las lentes es de 30 cm y la distancia entre la lente L2 y el vértice del espejo es de 20 cm. La lente L1 es plano-cóncava de potencia 5 dioptrías y la lente L2 es plano-convexa de radio 10 cm e índice de refracción 1.5. Se sabe que la imagen dada por el sistema de un objeto situado 20 cm a la izquierda de L1 es real y está situada a 12 cm del espejo. Determinar:
a) El radio de curvatura del espejo ¿Es un espejo cóncavo o convexo?
b) ¿Cuál es el carácter de la imagen?
Después se desplaza la lente L2 y se yuxtapone con la L1 pudiendo hacerse la unión bien por las caras planas o bien por las curvas.
c) ¿Cuál es la potencia de la lente resultante? Si el objeto y el espejo permanecen donde estaban inicialmente.
d) ¿Cuál es el carácter de la nueva imagen?
e) ¿Cambiaría el carácter de la imagen si fuera L1 la que desplazáramos hasta L2? Justificar las respuestas.

Problema de Óptica geométrica. Aparece en la convocatoria de JUL2009.

Un sistema óptico está formado por dos lentes, L1, biconvexa, de radios iguales, y distancia focal 20 cm, y L2, situada a su derecha, sobre el mismo eje, y a una distancia de 42 cm. Un objeto se encuentra 30 cm a la izquierda de L1. a) Determinar la distancia focal de L2 si la imagen final tiene el mismo tamaño que el objeto y es invertida respecto de él. b) A continuación se elimina la lente L2, y se yuxtapone a L1 otra lente L3 (el objeto se mantiene a 30 cm de las lentes). Calcula la distancia focal de esta nueva lente L3 si la imagen final dada por el sistema es invertida y mide el 80% del objeto. c) La lente L3 es cóncavo-convexa con índice de refracción 1.5 y sus radios están en relación 1 a 2. ¿Cuál es el valor de dichos radios?

Problema de Óptica geométrica. Aparece en la convocatoria de SEP2003.

Un sistema óptico está formado por dos lentes, la primera convergente de 60 cm de focal y la segunda divergente, separadas por 20 cm. a) Determinar la potencia de la segunda lente si estando el objeto a 15 cm de la lente convergente la imagen final dada por el sistema es 3.75 veces menor que el objeto; b) ¿cuál es el carácter de la imagen? c) la lente divergente está formada a su vez por dos lentes yuxtapuestas, una biconvexa de índice de refracción 1.2 y radios iguales y otra cóncavo-convexa de índice de refracción 1.8 y cuyos radios están en relación 1 a 3. Determinar los radios de curvatura de las lentes que componen la divergente; d) si en lugar de la lente divergente colocamos un espejo esférico en su misma posición, ¿qué radio debe tener dicho espejo para que el carácter y tamaño de la imagen siga siendo igual que antes? ¿Se trata de un espejo cóncavo o convexo?

Problema de Óptica geométrica. Aparece en la convocatoria de JUN2002.

Un sistema óptico está formado por tres elementos, una lente convergente cóncavo-convexa de 20 dioptrías (índice de refracción 1.5 y radios en relación 1 a 3), una lente bicóncava de 12 cm de focal (índice de refracción 1.6 y radios iguales) y un espejo convexo de 168 cm de radio, situados en este orden. La distancia entre la lente convergente y el vértice del espejo es de 54 cm. Se coloca un objeto 10 cm a la izquierda de la primera lente. a) Determinar las dos posibles posiciones de la lente divergente si se desea que la imagen final sea virtual y se encuentre a 21 cm del vértice del espejo; b) de entre las dos posiciones obtenidas en el apartado anterior, ¿cuál hay que elegir si además se desea que la imagen tenga un tamaño igual a la cuarta parte del tamaño del objeto? c) A continuación desplazamos la lente divergente hasta ponerla en contacto con la convergente. Determinar la posición y carácter de la nueva imagen. d) Calcular los radios de curvatura de las dos lentes.

Problema de Óptica geométrica. Aparece en la convocatoria de JUN2005.

Un sistema óptico está formado por una lente bicóncava L1, una convergente L2 de 10 dioptrías y un espejo cóncavo de 72 cm de radio, situados en este orden sobre un mismo eje. L1 está formada por dos lentes plano-cóncavas yuxtapuestas del mismo radio e índices de refracción 1.6 y 1.5 unidas por su cara plana. Se fija la posición de L2 situándola a 20 cm de L1 y a 75 cm del espejo. Si un objeto de 10 cm de altura colocado 20 cm a la izquierda de L1 da una imagen final real a 90 cm del espejo, ¿cuál es el radio de las lentes que componen L1? Determinar el tamaño y carácter de la imagen final.

Problema de Óptica geométrica.

Un sistema óptico está formado por una lente biconvexa de 5 dioptrías e índice de refracción 1.6 y una lámina de vidrio de 30 cm de espesor, índice de refracción 1.5 y cuyas caras son la primera convexa (de radio desconocido) y la segunda cóncava de 30 cm de radio. Se coloca un objeto a 40 cm de la lente. a) Determinar el radio de curvatura de la primera cara de la lámina de vidrio para que la imagen final sea invertida, tenga el mismo tamaño que el objeto y se forme justo en la primera cara de la lámina de vidrio. b) ¿Cuál debe ser en este caso la separación entre la lente y la primera cara de la lámina? c) Determina el radio de curvatura de las caras de la lente biconvexa si se sabe que están en relación 1 a 2. d) Se desea que la lente tenga la misma potencia pero distinto carácter. Para ello, se coloca otra lente de índice de refracción 1.4 yuxtapuesta a la biconvexa, de modo que ambas lentes tengan en común uno de los radios. Determina la potencia de esta lente y los radios de curvatura de sus caras.

Problema de Óptica geométrica. Aparece en la convocatoria de JUN2001.

Un sistema óptico está formado por una lente convergente de distancia focal 10 cm y un espejo cóncavo de 3 m de radio. A la izquierda de la lente hay un objeto de 10 cm de longitud que forma un ángulo de 30o con el eje del sistema y cuyo pie dista 20 cm de la lente. La distancia entre la lente y el vértice del espejo es 100 cm. a) Determinar la posición de la imagen final y el ángulo que dicha imagen forma con el eje del sistema óptico; b) se pretende sustituir la lente y el espejo por una única lente convergente que dé una imagen del objeto de tal modo que la distancia entre la proyección del extremo (punto B) y su imagen sea la misma que en el apartado anterior. Calcular la distancia focal y la posición (distancia al objeto) de dicha lente; c) si dicha lente es cóncavo-convexa con un índice de refracción de 1.5 y sus radios de curvatura están en la relación 1 a 3 calcular dichos radios. Todas las lentes pueden considerarse delgadas.

Problema de Óptica geométrica. Aparece en la convocatoria de JUN2007.

Un termómetro de resistencia de platino permite realizar determinaciones precisas de temperatura a partir de la medida de la resistencia eléctrica R del termómetro y de la relación temperatura-resistencia. Cuando la temperatura t viene dada en la escala Celsius, esta relación termométrica se conoce como ecuación de Callendar-Van Dusen y toma la forma:

donde: 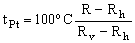es la denominada temperatura del platino y Rh y Rv son, respectivamente, los valores de R en los puntos de hielo (0 oC) y de vapor de agua (100 oC). Las constantes δ y β son características del platino y están relacionadas con el comportamiento no lineal de la variación de R con t; si δ y β fueran nulas, la variación sería lineal y la temperatura del platino coincidiría con la temperatura Celsius. Considerando un termómetro para el que Rh=24.236 Ω y Rv=34.452 Ω, se pide: a) determinar las constantes δ y β teniendo en cuenta que en los puntos de ebullición normal del azufre (444.674 oC) y del oxígeno (-182.962 oC) la resistencia del termómetro es de 67.417 Ω y 5.927 Ω respectivamente, y que β=0 oC para t>>0 oC; b) calcular la temperatura correspondiente a una resistencia R=25.186 Ω.

Problema de Calor y Primer Principio de la Termodinámica.