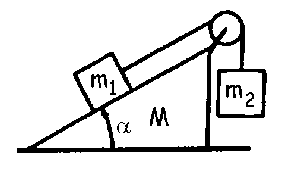
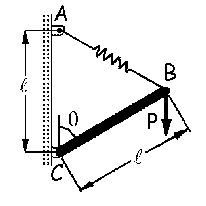
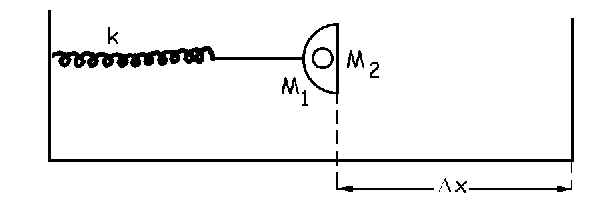
Cuestion de Dinámica de la Partícula.
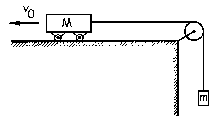
En el esquema representado en la figura no existe rozamiento. Si T1=4 N, determinar F.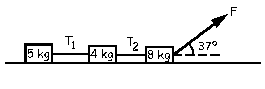
Cuestion de Dinámica de la Partícula.
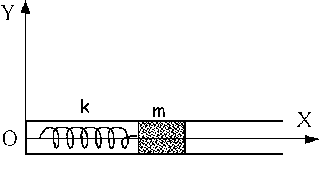
Problema de Movimiento Oscilatorio. Aparece en la convocatoria de SEP2000.
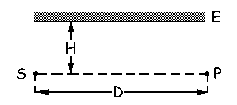
Problema de Reflexión y Refracción de Ondas.
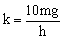 , donde g es la aceleración de la gravedad y h=60 m la altura del puente respecto a la superficie del agua, determinar: a) la longitud que debe tener la cuerda para que el que salta apenas llegue a la superficie vuelva hacia arriba (despréciese cualquier efecto debido a la fricción y a la altura del deportista); b) ahora consideremos que después del primer salto debido a la fricción, la amplitud de las oscilaciones va disminuyendo. ¿A qué altura sobre el agua estará el saltador cuando hayan cesado las oscilaciones?
, donde g es la aceleración de la gravedad y h=60 m la altura del puente respecto a la superficie del agua, determinar: a) la longitud que debe tener la cuerda para que el que salta apenas llegue a la superficie vuelva hacia arriba (despréciese cualquier efecto debido a la fricción y a la altura del deportista); b) ahora consideremos que después del primer salto debido a la fricción, la amplitud de las oscilaciones va disminuyendo. ¿A qué altura sobre el agua estará el saltador cuando hayan cesado las oscilaciones?