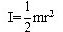Problemas archivo - Página 89 de 120 -

Un cuerpo de masa m se desliza hacia abajo por un plano inclinado de ángulo α. El coeficiente de rozamiento es μ. Hallar la rapidez de cambio de la energía cinética más la potencial al cabo de t segundos

Cuestion de Trabajo y Energía.

Un cuerpo de masa m se halla suspendido de un resorte helicoidal, habiéndose medido el tiempo empleado en 100 oscilaciones completas para los siguientes valores de m:

m (kg)	t de 100 oscilaciones (s)
1	115.3
2	162.25
3	198.7
7	303.5

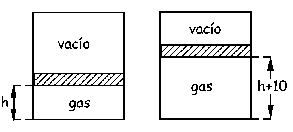
a) ¿Cuál es la constante recuperadora del resorte?; b) para una masa de 5 kg y sabiendo que la velocidad al pasar por la posición de equilibrio es de 5 m/s, calcular la aceleración al pasar por el punto de máxima elongación; c) una fuerza periódica actúa sobre esa masa de 5 kg. La fuerza de amortiguamiento es proporcional a la velocidad instantánea y vale 100 N cuando la velocidad es de 2.5 m/s. Calcular la ecuación del movimiento sabiendo que para t=0 la posición es 5 m y la velocidad es de -25 m/s.

Problema de Movimiento Oscilatorio.

Un décimo de mol de un gas perfecto se encuentra en la parte inferior del recipiente de la figura. El pistón tiene una superficie de 50 cm², pesa 100 kg y se encuentra situado a una altura h, siendo la temperatura inicial de 273 K. Se calienta el gas y el pistón sube 10 cm. Calcular la altura h, la temperatura final, la variación de energía interna y el calor suministrado.
Tómese c_v=5 cal/molK; 1 atm=1 kg/cm²; constante de los gases perfectos: R=2 cal/molK

Problema de Teoría Cinética de los Gases.

Un diapasón se coloca junto a un tubo hueco que contiene agua y se hace vibrar, obteniéndose un pitido intenso cuando la longitud de la columna de aire es 16 cm. Tomando la velocidad del sonido en aire, en las condiciones de la experiencia, igual a 340 m/s, calcular la frecuencia mínima de vibración del diapasón. Explíquese qué fenómenos físicos se consideran.

Cuestion de Movimiento Ondulatorio.

Un disco circular uniforme rueda sin deslizamiento con una velocidad v y encuentra un cambio brusco de dirección de movimiento al alcanzar el plano inclinado θ. Determinar la nueva velocidad v´ del centro del disco al iniciar la subida hacia arriba del plano, así como la fracción n de la energía inicial que se pierde a causa del contacto con el plano inclinado. Tomar θ=10^o.

Problema de Dinámica del Sólido Rígido.

Un disco de masa m y radio r rueda sin deslizar sobre la cara interior de una superficie cilíndrica de radio R. Sabiendo que el disco parte del reposo en la posición indicada en la figura, obtener las expresiones que proporcionan: a) la velocidad lineal del disco a su paso por B; b) el módulo de la reacción normal del suelo sobre el disco en B.

Problema de Dinámica del Sólido Rígido.

Un disco gira alrededor de un eje perpendicular a su plano en el sentido de las agujas del reloj con una aceleración angular uniforme de 1 rad/s²; en t=0 su velocidad angular es igual a cero. Un punto M oscila por uno de los diámetros del disco de tal modo que su coordenada vale x´=sen(πt) m, con t en segundos. Determinar, en el instante t=5/3 s las proyecciones de la aceleración absoluta del punto M sobre los ejes X´Y´ solidarios con el disco.

Problema de Cinemática de la Partícula.

Un disco gira con velocidad angular constante ω alrededor del eje que pasa por su centro y es perpendicular al plano del disco. Un punto M se desplaza por la cuerda AB a partir de su punto medio D con una velocidad relativa constante u. La distancia entre la cuerda y el centro del disco es igual a c. Hallar la velocidad y la aceleración absolutas del punto M en función de la distancia DM=x.

Problema de Cinemática de la Partícula.

Un disco homogéneo de 2 kg y r=0,3 m lleva enrollada una cuerda en su periferia y está sostenida por la mano de una persona que acelera hacia arriba sin que se mueva el centro de masas del disco. Determinar: a) la tensión de la cuerda; b) la aceleración angular; c) la aceleración de la mano. A continuación, dejamos caer el disco sin mover la mano; calcular: d) la aceleración del centro de masas; e) la aceleración angular de la cuerda; f) la tensión en la cuerda; g) la velocidad del centro de masas después de dar una vuelta completa.
Momento de inercia de un disco respecto de un eje que pasa por su centro:

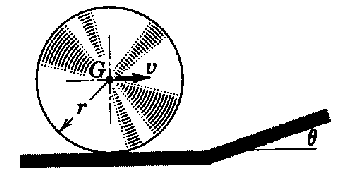
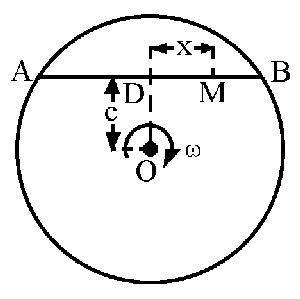
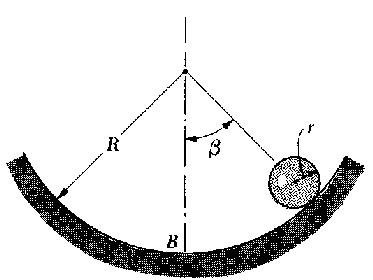
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de DIC2018.

Un espejo cóncavo de 0.5 m de distancia focal está frente a un espejo plano situado a 1.8 m del vértice del espejo cóncavo y perpendicular al eje del mismo. A 20 cm del espejo plano y entre éste y el cóncavo está situado un punto luminoso que se refleja primero en el espejo plano y luego en el esférico. Encontrar la posición de la imagen producida por el sistema y el aumento del mismo.

Problema de Óptica geométrica.