Dinámica del Sólido Rígido

Se tira hacia delante de la rueda representada en la figura mediante una fuerza constante F=260 N. El peso de la rueda es de 375 N y su radio de giro respecto al eje de la rueda (radio de giro centroidal) es de k=231 mm (ICM=mk2). La rueda va rodando sin deslizamiento por la superficie horizontal y en la posición representada lleva una velocidad angular de 15 rad/s en sentido horario. Determinar: a) la aceleración angular de la rueda y las componentes horizontal y vertical de la fuerza que ejerce la superficie sobre ella; b) el valor del mínimo coeficiente de rozamiento que evita el deslizamiento; c) la velocidad angular de la rueda cuando ha dado una vuelta completa.

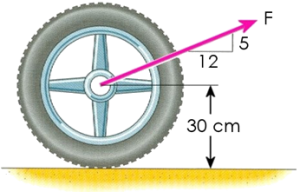
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2025.

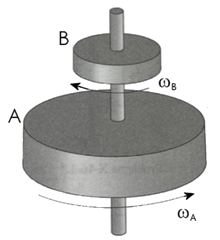
a) Explica qué se entiende por movimiento de rodadura (considera sólo la situación ideal). ¿Cuál o cuáles son las condiciones para que se produzca rodadura? (Explicita y explica las ecuaciones correspondientes).

b) La rueda de la figura, de 25 kg, tiene un momento de inercia respecto a su centro de masas de 1,1025 kgm2. Esta rueda gira sin deslizar en sentido horario y parte del reposo en la posición representada, girando 90º. El resorte tiene una longitud natural de 0,15 m y su constante es de 18 N/m. Calcula el alargamiento de los resortes en la posición inicial y final y la velocidad angular final de la rueda.

Cuestion de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2023.

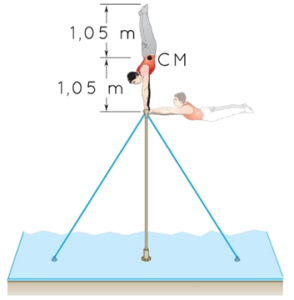
Una barra uniforme de longitud L=900 mm y masa m=4 kg está suspendida de un pasador en C, inicialmente en reposo. Una fuerza horizontal F=75 N se aplica en el extremo B tal como se indica en la figura. Sabiendo que d=225 mm determinar: a) la aceleración angular de la barra y las componentes de la reacción en C en el instante inicial; b) si la fuerza F se mantiene aplicada perpendicularmente a la varilla y en el extremo B durante 45º mientras la varilla rota y después se elimina, determinar la velocidad angular de la varilla cuando llegue a la posición horizontal.

Momento de inercia de una barra respecto de un eje que pasa por su centro de masas: (1/12) mL2.

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2025.

a) ¿Cómo se define el momento de inercia de un sólido rígido? ¿Qué significado tiene para la rotación? En relación con el momento de inercia, i) enuncia el teorema de Steiner e indica en qué situaciones se aplica; ii) explica qué se entiende por radio de giro. b) Se unen cuatro partículas de masa m=10 g mediante varillas sin masa, formando un rectángulo de lados 20 y 40 cm. El sistema gira alrededor de un eje perpendicular al plano de la figura y que pasa por el centro de masas. Calcula el momento de inercia del sistema respecto de un eje perpendicular al plano de la figura y que pase por una de las masas.

Cuestion de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.

a) ¿Qué es el momento de una fuerza? Si el momento de las fuerzas exteriores es nulo, ¿qué otras magnitudes permanecen constantes? Explícalo con un ejemplo. b) El disco A de la figura gira con una velocidad angular de 4 rad/s. El disco B, que tiene un momento de inercia tres veces menor que el de A(ambos respecto del eje de giro), gira con una velocidad angular de 8 rad/s en sentido contrario al de A. Si de pronto, estando en esas condiciones se acoplan ambos discos para que giren juntos, ¿cuál es la velocidad angular final del conjunto?

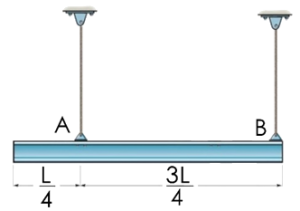
Cuestion de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.

En el instante en que el resorte está sin deformar, el paquete de 40 kg de la figura (1) tiene una velocidad de 4 m/s y desliza sobre una superficie de coeficiente de rozamiento m=0,6. A partir de este punto, determina: a) la distancia d que se mueve el paquete hacia abajo del plano inclinado antes de detenerse momentáneamente; b) la distancia que se movería en las mismas condiciones (resorte sin elongar y velocidad de 4 m/s sobre un suelo de coeficiente de rozamiento 0,6) un disco de idéntica masa y 0,3 m de radio, tal como el que aparece en la figura (2); c) la aceleración angular y la fuerza de rozamiento en el instante calculado en el apartado b); d) la elongación del resorte y la fuerza de rozamiento en el instante en que la velocidad del disco es máxima. Momento de inercia de un disco respecto de un eje perpendicular al mismo y que pasa por su centro 1/2(mR2).

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.

Un gimnasta de 75 kg está ejecutando una serie de vueltas completas en la barra horizontal. En la posición representada su velocidad angular es menospreciablemente pequeña y de sentido horario y su cuerpo se mantiene rígido y recto al girar hacia abajo. Suponiendo que durante el giro momento de inercia del gimnasta respecto de su centro de masa es de 15,1875 kgm2, hallar la velocidad angular y la fuerza que soportan sus manos tras haber rotado: a) 90º; b) 180º.

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de FEB2023.

La barra delgada uniforme de la figura tiene un peso de 20 N y una longitud de 1 m y está soportada por dos cables paralelos e iguales de 0,5 m de longitud. a) Se suelta la barra desde el reposo con los cables formando un ángulo de 60º respecto de la vertical. ¿Qué velocidad lleva la barra cuando en el movimiento posterior los cables formen un ángulo de 30º respecto de la vertical? (0,5 puntos) b) ¿Cuánto valen las tensiones en los cables al pasar por esta posición? (30º) (0,75 puntos). c)  Si se coloca la barra en reposo en la posición que indica la figura y se corta el cable B, determinar la tensión en el cable A en el instante inmediatamente después de la rotura (0,75 puntos).

Momento de inercia de una barra respecto de un eje perpendicular a la misma que pasa por su centro: 1/12 (mL2).

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.