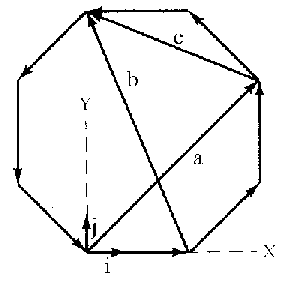
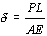Dado el vector A=xy2i+(x2z-y2)j+2x2zyk, calcular dA.
Problema de Introducción (Magnitudes y Vectores).
Problema de Introducción (Magnitudes y Vectores).
Problema de Introducción (Magnitudes y Vectores).
Cuestion de Introducción (Magnitudes y Vectores).
Problema de Introducción (Magnitudes y Vectores).
Problema de Introducción (Magnitudes y Vectores).
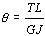
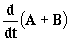 ; b)
; b) 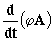 ; c)
; c) 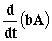 ; d)
; d) 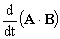 ; e)
; e) 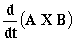 ; f)
; f) 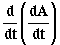 .
.