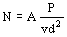Introducción (Magnitudes y Vectores)

La viscosidad η de un fluído resulta ser una magnitud importante en mecánica de fluídos. Se define la viscosidad mediante la relación:

a) ¿Cuáles son las dimensiones de la viscosidad? b) expresar la unidad mks de la viscosidad, el decapoise, en función de las unidades mks primarias.

Problema de Introducción (Magnitudes y Vectores).

¿Cuáles de los siguientes vectores son mutuamente perpendiculares? Cada conjunto de tres números da las componentes de un vector.

A=(2, 1, 1); B=(0, 0, 2); C=(1, -2, 0); D=(1, 1, -3); E=(9, 5, 3)

Problema de Introducción (Magnitudes y Vectores).

El vector v, expresado en componentes cartesianas viene dado por v=a[1+cos(t)]i+a sen(t)j siendo a una constante y t una variable escalar. Determinar las componentes cartesianas y las componentes intrínsecas de la derivada del vector v respecto a la variable t, comprobando la identidad de ambos resultados. Para que valores de t se verificará ?

Problema de Introducción (Magnitudes y Vectores).

¿Cuál es la masa en gramos de un cuerpo que pesa exactamente 1 dina en un punto en el que g=9,81 m/s²? ¿Cuál es la masa de un cuerpo que pesa 1 N en ese punto? ¿Cuál es la masa en slug de un cuerpo que pesa 1 libra en ese punto

Problema de Introducción (Magnitudes y Vectores).

Utilizando un sistema que tenga como unidades fundamentales la presión de 1 kp/cm ², la densidad absoluta del mercurio a 0^o C 13.6 g/cm³ y la aceleración de la gravedad 9.8 m/s², determinar la ecuación dimensional del tiempo y el valor de su unidad en segundos.

Problema de Introducción (Magnitudes y Vectores).

Hallar el coseno del ángulo θ existente entre A=3i+j+2k y B=-3i+j+2k.

Problema de Introducción (Magnitudes y Vectores).

Dados los vectores a=(2,3,1), b=(0,1,1) y c=(3,3,3) aplicados respectivamente en los puntos A=(1,0,2), B=(1,2,1) y C=(0,0,0) determinar: a) su suma; b) su momento resultante en el origen O; c) su momento resultante en el punto O´=(1,1,1).

Problema de Introducción (Magnitudes y Vectores).

La densidad del acero vale 7.8 g/cm³. Expresarla en el Sistema Internacional y en los sistemas técnico, gravitacional inglés y absoluto inglés.

Problema de Introducción (Magnitudes y Vectores).

Admitiendo que el número N de cables necesarios para una transmisión funicular viene dado por la expresión:

siendo P la potencia transmitida, v la velocidad de los cables y d su diámetro, determinar si A variará al cambiar las unidades empleadas, y en caso afirmativo, la relación entre los valores de A empleando el Sistema Internacional y otro en que la potencia se mida en caballos de vapor, la velocidad en m/s y el diámetro en mm.

Problema de Introducción (Magnitudes y Vectores).

Demostrar que si uno de los vectores del producto escalar A*B se multiplica por un escalar c, resulta sin variación el ángulo formado entre A y B.

Problema de Introducción (Magnitudes y Vectores).
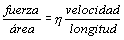
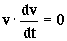