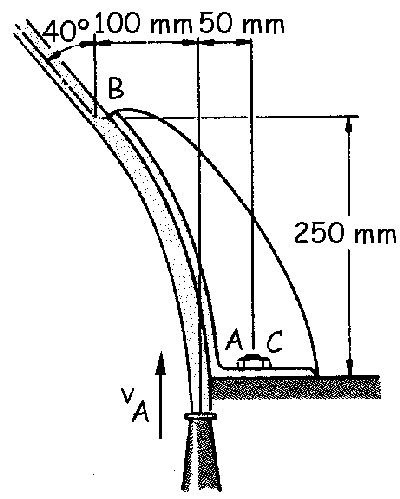
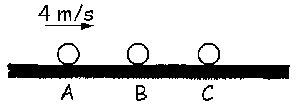Problema de Dinámica de la Partícula.
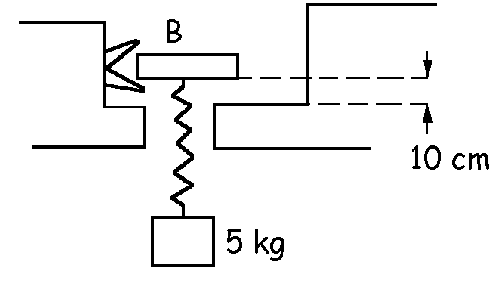
Problema de Dinámica de los Sistemas de Partículas.
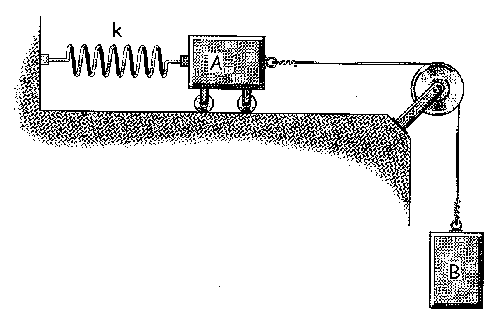
Determinar la frecuencia de oscilación del objeto de masa m en los dos casos de la figura.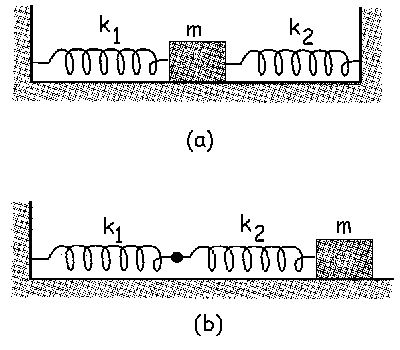
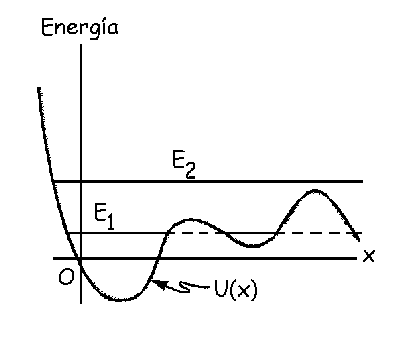
Problema de Movimiento Oscilatorio.
Problema de Introducción (Magnitudes y Vectores).
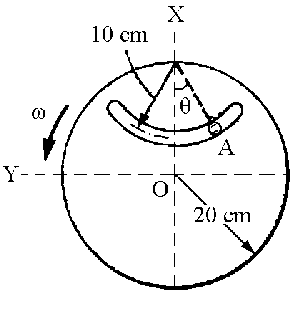
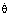 =3 rad/s,
=3 rad/s,  =5 rad/s2, ω=10 rad/s y
=5 rad/s2, ω=10 rad/s y  =25 rad/s2: a) la velocidad y aceleración del pasador A; b) la fuerza que la ranura ejerce sobre el pasador.
=25 rad/s2: a) la velocidad y aceleración del pasador A; b) la fuerza que la ranura ejerce sobre el pasador.