Física I

Dado un vector deslizante F=-i+2j+3k cuya recta de acción pasa por el punto P=(2, 1, 1), y el par de momento M=4i+2j, reducir dicho sistema a un vector único (de ser posible) aplicado en un punto del plano XY, cuyas coordenadas deben determinarse.

Cuestion de Introducción (Magnitudes y Vectores).

La vigueta uniforme de acero tiene 4.9 m de largo y pesa 453.6 kg. Si el cable soportante CB se rompe, determinar la tensión T en el cable AC un instante después de la rotura. La vigueta puede considerarse como una barra rígida delgada.

Problema de Dinámica del Sólido Rígido.

El bloque cuadrado macizo se apoya en el plano horizontal mediante un pequeño cilindro con rozamiento despreciable. Se suelta el bloque desde el reposo en la posición que se muestra. Calcular la velocidad angular ω del bloque y la velocidad lineal de la esquina O cuando la C alcance la superficie horizontal.

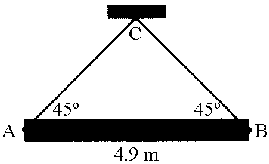
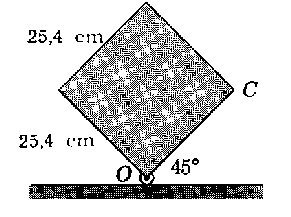
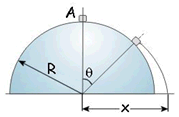
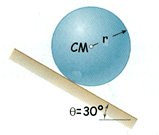
Problema de Dinámica del Sólido Rígido.

¿Cómo es el movimiento debido a fuerzas centrales?

Cuestion de Dinámica de la Partícula.

¿Cómo podemos trasladar una fuerza aplicada en un punto de un sólido a otro punto sin que cambien sus efectos? Justifica la respuesta.

Cuestion de Dinámica del Sólido Rígido.

¿Cómo se puede reducir un sistema de vectores deslizantes (V.D.)?. Mostrarlo realizando un esquema explicando los pasos que se dan. ¿Qué sistemas de V.D. se pueden reducir a un único vector?

Cuestion de Introducción (Magnitudes y Vectores).

Deducir la expresión de la frecuencia de vibración de un péndulo de torsión al girar un ángulo θ muy pequeño alrededor de su posición de equilibrio.

Cuestion de Movimiento Oscilatorio.

Un cubito de hielo de 50 g de masa resbala por una superficie esférica de radio R=0,5 m. El cubito parte del punto más alto A con velocidad nula. El rozamiento entre el cubito y la esfera es despreciable. Calcular: a) el ángulo θ para el cual el cubito pierde el contacto con la superficie esférica; b) la aceleración del cubito cuando θ=30^o; c) la reacción de la esfera en este momento; d) la distancia x respecto del punto A a la cual el cubito llega al suelo; e) la velocidad del cubito cuando llega al suelo.

Problema de Trabajo y Energía. Aparece en la convocatoria de ENE2014.

Se suelta sin velocidad inicial una esfera de masa m y radio r sobre un plano inclinado. Hallar: a) el valor mínimo del coeficiente de rozamiento compatible con un movimiento de rodadura; b) la velocidad del centro de la esfera tras haber rodado 4 m en estas condiciones; c) la aceleración lineal del centro de masas y la aceleración angular de la esfera si el coeficiente de rozamiento fuera 0,1 y el radio de la esfera 20 cm; d) la velocidad de la esfera si hubiera recorrido 4 m sobre un plano sin rozamiento inclinado 30º.
Momento de inercia de una esfera respecto de un eje que pasa por su centro de masas: 2/5(mr²)

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de JUN2015.

Definir el momento angular de una partícula respecto de un punto. A partir de la generalización del momento angular de una partícula deducir la expresión del momento angular de un sólido rígido que gira respecto de un eje fijo (L=Iω). Definir la expresión del momento de inercia.

Cuestion de Dinámica del Sólido Rígido.